
在上篇文章中,我們學會將程式碼分為 Actions、Calculations 與 Data 三類,並理解到 Calculations 是我們程式中穩定、可靠的核心。今天這篇會再深入探討 Calculations,也就是我們常聽到的純函數 (Pure Function)。
到底是什麼樣的特質,讓一個函式如此「純粹」又可靠呢?
一個函式要被稱為「純函數」,必須遵守以下兩條定律:
以簡單的加法純函數舉例如下:
const add = (a, b) => a + b;
不論呼叫 add(2, 3) 多少次,它永遠會回傳 5。而且它除了回傳結果之外,沒有對外部世界做任何其他事情,沒有產生任何副作用。
接著詳細一點拆解這兩個規則,看看它們在實務中代表什麼。
「相同輸入,相同輸出」聽起來理所當然,但其實很多我們常用的函式都違反了這條定律。
舉例如下:
// 每次呼叫,結果都不同
Math.random(); // 第一次可能是 0.289...
Math.random(); // 第二次可能是 0.215...
// 結果跟「何時」呼叫有關
new Date(); // Tue Aug 05 2025 09:21:00 GMT+0800...
像 Math.random() 和 new Date() 這種函式,它們的輸出會隨著呼叫次數、呼叫時間或內部狀態而改變,因此它們是不純的。
這是純函數最關鍵的一條規則。前面文章曾提過,副作用是指一個函式除了回傳值之外,對其外部環境所做的任何可觀察的改變。
常見的副作用包括:
console.log)fetch)來看一個 JavaScript 中的例子:slice 和 splice
slice (純函數)slice 會回傳一個陣列的片段,但它不會修改原始陣列。
const xs = [1, 2, 3, 4, 5];
xs.slice(0, 3); // [1, 2, 3]
xs.slice(0, 3); // [1, 2, 3]
console.log(xs); // [1, 2, 3, 4, 5] <-- 原始陣列保持不變
不管呼叫 xs.slice(0, 3) 幾次,得到的結果都一樣,而且原始的 xs 陣列也保持不變。
splice (不純的函式):splice 則會直接修改原始陣列,這就產生了副作用。
const xs = [1, 2, 3, 4, 5];
xs.splice(0, 3); // [1, 2, 3]
xs.splice(0, 3); // [4, 5] <-- 🔺 第二次呼叫,結果不同了
console.log(xs); // [] <-- 🔺 原始陣列被清空了
因為 splice 每次呼叫都會改變 xs,所以即使我們用相同的參數 (0, 3) 呼叫它,每次得到的結果都不同。這就是不純的函式帶來的不可預測性。
另外補充,現代 JavaScript 越來越重視不可變性 (immutability),並提供了許多原生函式的純函數版本。例如,針對 splice,現在有了 toSpliced(),它的作用相同,但會回傳一個新的陣列,不會動到原始陣列:
const xs = [1, 2, 3, 4, 5];
xs.toSpliced(0, 3); // [4, 5]
xs.toSpliced(0, 3); // [4, 5] <-- ✅ 每次結果都一樣
console.log(xs); // [1, 2, 3, 4, 5] <-- ✅ 原始陣列保持不變
同樣的,傳統的 sort() 會直接在原陣列上排序 (不純的函式),而新的 toSorted() 則會回傳一個排序後的新陣列 (純函數)。
splice 這種不可預測的行為,不僅是程式設計上令人困擾的地方,它其實還違反了我們在國中數學課學的「函數」的根本定義。
其實「純函數」的概念與我們在國中數學課學的「函數」定義完全相同。數學上的函數,是一種特殊的對應關係:「每一個輸入值,都只會對應到一個確切的輸出值。不同輸入可以有相同的輸出值。」
熟悉的 x 對應 y 的函數關係圖如下,這是 x 到 y 的合法 function 關係,可以把 x 想性成純函數的輸入值,y 當作輸出值,一個 x 對應一個 y 值,等於一個輸入值只會對應一個輸出值。
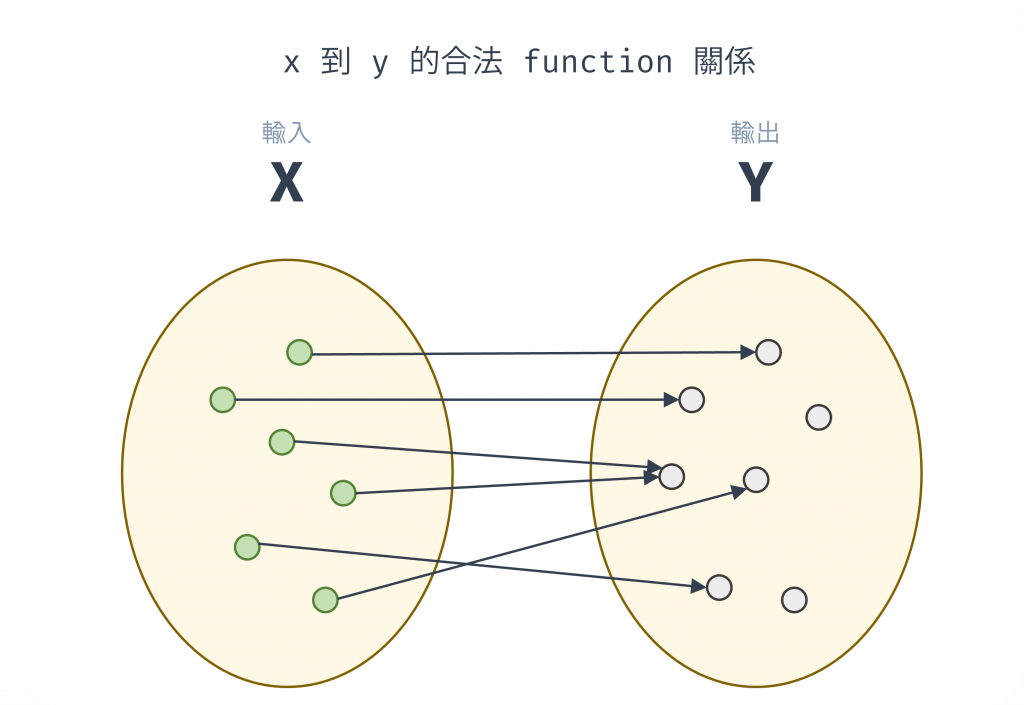
圖 1 x 到 y 的合法 function 關係(資料來源: 自行繪製)
一個輸入不能對應到多個輸出。splice 的行為就違反了這個原則,因為同一個操作 (xs.splice(0, 3)) 卻產生了不同的結果。而 slice 和 toSpliced 則完美地符合數學函數的定義。下圖就顯示由 x 到 y 的非 function 的關係,非 function 關係的原因是因為輸入值的 5 指向了多個輸出,就像是對 (0, 3) 這個相同輸入值,splice 卻給了多個輸出一樣。
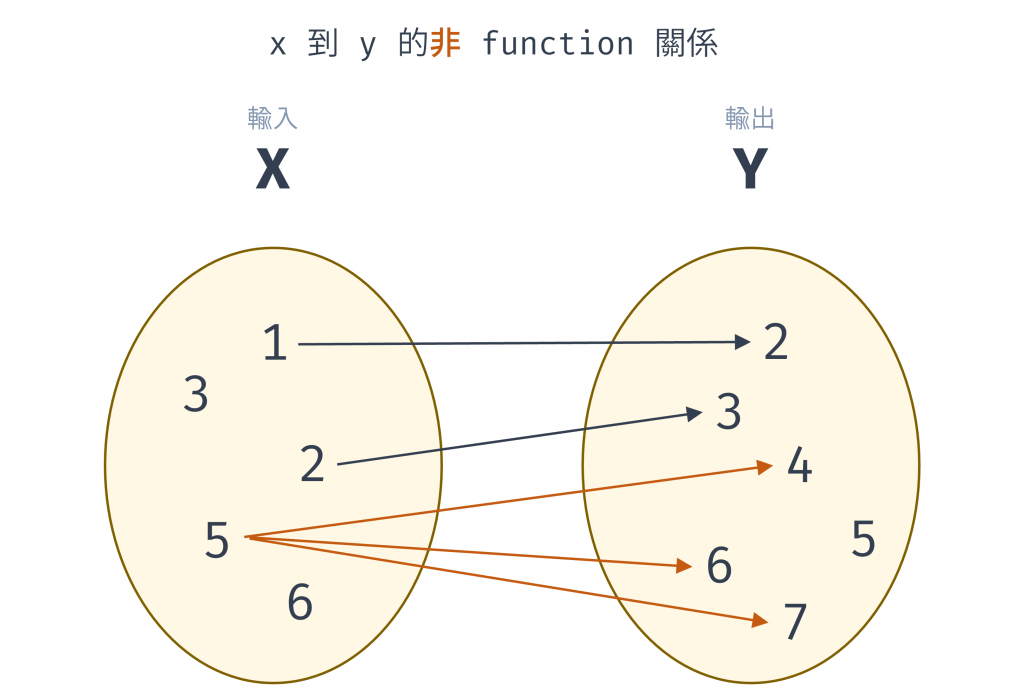
圖 2 x 到 y 的非 function 關係(資料來源: 自行繪製)
可以說純函數就是數學意義上的函數。這也是為什麼 FP 程式設計師如此推崇純函數,因為如果我們的程式碼都可以盡量寫成純函數,就可以借鏡數學理論中可組合、可預測的特性,讓程式碼變得更可控。
是什麼機制確保了純函數能像數學函數一樣運作呢?答案在於它處理資訊的方式。
在一個函式中,會有輸入和輸出值之分,輸入 (inputs) 指的是函式在運算時需要的外部訊息,從函式外進來的訊息都是輸入;輸出(outputs)則是函式所產生的資訊或動作,從函式裡出去的訊息、效果都是輸出。而我們呼叫函式的目的就是為了取得輸出,舉例如下:
var total = 0;
function add_to_total(amount){ // 傳入的參數是輸入
console.log("Old total: " + total); // 讀取全域變數 total 的值為輸入,console 將結果印出是輸出
total += amount; // 修改全域變數是輸出
return total; // 傳回值是輸出
}
再進一步區分,函式的輸入與輸出有顯性、隱性之分,說明如下表:
| 類型 | 說明 |
|---|---|
| 顯性輸入(explicit inputs) | 傳入參數(arguments) |
| 顯性輸出(explicit outputs) | 傳回值 |
| 隱性輸入(implicit inputs) | 利用其他非參數管道的輸入 |
| 隱性輸出(implicit outputs) | 利用其他非傳回值管道的輸出 |
延續上述範例可這樣分:
var total = 0;
function add_to_total(amount){ // 參數是顯性輸入
console.log("Old total: " + total); // 讀取全域變數是隱性輸入,console 是隱性輸出
total += amount; // 修改全域變數是隱性輸出
return total; // 傳回值是顯性輸出
}
而根據我們對純函數的了解,再結合顯性和隱性輸入輸出的定義,我們其實可以發現一個規律:
「純函數所有的依賴都來自於顯性的輸入 (Explicit Inputs),也就是它的參數;而它對世界的唯一影響就是它的顯性輸出 (Explicit Output),也就是它的回傳值。」
相對地,不純的函式 (也就是 Actions) 常常依賴隱性的輸入 (Implicit Inputs),或是造成隱性的輸出 (Implicit Outputs) 。
依賴隱性輸入的例子如下:
let taxRate = 0.05; // 隱性輸入
// 不純的函式,依賴外部變數
const calculateTaxImpure = (price) => {
return price * taxRate;
};
calculateTaxImpure 的結果不僅取決於 price,還偷偷地依賴了外部的 taxRate。如果 taxRate 在程式的其他地方被改變,這個函式的行為就會變得不可預測,增加我們的認知負擔。
如果將 calculateTaxImpure 改為顯性輸入:
// 純函數,所有依賴都來自參數
const calculateTaxPure = (price, rate) => {
return price * rate;
};
這個函式現在就變得完全獨立自主,所有輸入都是顯性的,它的行為只跟我們傳給它的東西有關。
因為純函數沒有任何外部依賴或副作用,測試它們變得非常簡單。我們只需要給定輸入,然後驗證輸出是否符合預期即可,測試前不需 setup、測試後不需 assert 狀態,省卻許多麻煩。
當你看到一個純函數的呼叫時,你完全不用擔心它會不會在你看不到的地方引發奇怪的 bug。這個特性被稱為「引用透明性 (Referential Transparency)」,意思是你可以把一個純函數的呼叫,直接用它的回傳值取代,而不會改變整個程式的行為。
例如,程式中的 add(3, 4) 可以直接被 7 取代。這個特性讓我們可以用「等式推導」的方式來分析程式碼,就像在解數學題一樣。
以下舉一個引用透明性的例子,情境是計算一張訂單的最終金額,如果使用者是 Prime 會員,則免運費;否則需要加上 5 元的運費。
const alice = { name: 'Alice', isPrimeMember: false };
const bob = { name: 'Bob', isPrimeMember: true };
const order = { total: 80 };
// 純函數:回傳一個加上運費的新訂單物件
const addShippingFee = (ord) => ({...ord, total: ord.total + 5 });
// 純函數:檢查是否為 Prime 會員
const isPrimeMember = (usr) => usr.isPrimeMember;
// 純函數:組合前兩者來計算最終金額
const calculateFinalTotal = (usr, ord) => (isPrimeMember(usr)? ord : addShippingFee(ord));
console.log(calculateFinalTotal(alice, order)); // { total: 85 }
console.log(calculateFinalTotal(bob, order)); // { total: 80 }
addShippingFee、isPrimeMember 和 calculateFinalTotal 皆為純函數,具備引用透明性,因此可用「等式推導 (equational reasoning)」來分析 calculateFinalTotal(alice, order) 的結果,步驟拆分如下:
calculateFinalTotal:將函式呼叫替換為其內部的邏輯
calculateFinalTotal(alice, order) 可直接用 isPrimeMember(alice)? ord : addShippingFee(order) 表示isPrimeMember(alice)? order : addShippingFee(order)
isPrimeMember:將 isPrimeMember(alice) 替換為其函式內容
isPrimeMember(alice) 可直接用 alice.isPrimeMember 表示alice.isPrimeMember? order : addShippingFee(order)
alice.isPrimeMember 換成它的實際值 false
false? order : addShippingFee(order)
false,三元運算式只會剩下 else 的部分
addShippingFee(order)
addShippingFee:最後,將 addShippingFee(order) 替換為其函式內容
addShippingFee 可直接用 {...order, total: order.total + 5 } 表示({...order, total: order.total + 5 })
order 的值,我們就能得到最終結果:
{ total: 85 }
經過等式推導整理後,calculateFinalTotal(alice, order) 簡化後只是 alice 的 order.total + 5,過程完全可推理,因為所有函式都是純的,我們可以像這樣一步步替換和簡化,有信心地推導出最終結果。
引用透明性帶來許多優點,例如:
因為純函數對相同的輸入永遠有相同的輸出,我們可以把計算成本高的純函數結果快取起來。如果下次又用相同的參數呼叫它,就可以直接回傳快取的結果,這是一種叫做「記憶化 (Memoization)」的效能優化技巧。
// 假設 memoize 是一個幫我們快取結果的輔助函式
const slowSquare = memoize(x => {
//... 假設這裡有很複雜的計算...
return x * x;
});
slowSquare(5); // 第一次呼叫,執行複雜計算,回傳 25
slowSquare(5); // 第二次呼叫,直接從快取回傳 25,不需計算
另也補上基本的 memoize 實作如下:
const memoize = (f) => {
const cache = {}; // 儲存快取值
return (...args) => { // 回傳一個 function,外部使用時會呼叫此 function 並傳入參數,例如這 function 會作為上方的 slowSquare,執行 slowSquare 傳入的參數就是 args
const argStr = JSON.stringify(args); // 轉換參數為字串,作為快取的 key
cache[argStr] = cache[argStr] || f(...args); // 如果相同輸入已經計算過,則直接回傳快取值,否則計算並存入快取
return cache[argStr];
};
};
純函數是自給自足的,它需要的所有東西都透過參數明確地傳遞進來,也就上前面所說的顯性輸入。這就像是函式自帶了「使用說明書」,光看函式的參數就能理解它的依賴。以下說明依賴關係不明確和明確的函式。
看到 signUp,我們無法確定它會對系統造成什麼影響,因為 saveUser 和 welcomeUser 的依賴是隱藏的,也就是他們有隱性輸入和隱性輸出。
// 我們不知道 saveUser 和 welcomeUser 內部依賴了什麼
const signUp = (attrs) => {
const user = saveUser(attrs);
welcomeUser(user);
};
此版本的程式清楚地告訴我們,signUp 需要一個資料庫連線 (Db) 和一個郵件服務 (Email) 才能運作。這種「依賴注入 (Dependency Injection)」的方式讓函式變得非常靈活,我們可輕鬆更換 Db 或 Email,函式也會更容易重複使用,不同應用場景下可使用不同依賴。
// 所有依賴 (Db, Email) 都被明確地傳入
const signUp = (Db, Email, attrs) => {
const user = saveUser(Db, attrs);
welcomeUser(Email, user);
};
補充:依賴注入
關於依賴注入我在[心得] Tech Book Community 線下小聚 -【Zet】React Render Props文章中有提到,簡單來說依賴注入(dependency injection)意思是將系統需要的資料由外部傳入,而不是在內部自行建立或寫死,目的是將邏輯與資源分離。
上面所說的是自我文件化,純函式可透過顯性輸入輸出作為自己本身的文件。
再來談 Portability(可移植性),可移植性代表函式可以序列化並透過網路傳輸或是在 Web Worker 中執行。因為相較命令式程式設計 (imperative programming),純函數不依賴環境狀態,可在任何地方執行。
因為純函數不依賴共享的狀態,也不會去修改外部的資料,所以它們可以非常安全地被並行執行,完全不用擔心會發生「競爭條件 (race condition)」這類棘手的併發問題。
舉例來說,在瀏覽器中,我們可以放心地將純函數丟到 Web Worker 中去執行,而不用擔心狀態同步的問題。
小小總結今天對純函數的認識如下:
然而,純函數仍有一些挑戰,例如在純函數中,我們需手動處理資料傳遞(arguments 在函式間傳遞),不能在純函數使用狀態(state),也不能產生副作用(effects),但實務上很難完全做到,這代表我們不可能讓程式中所有的函式都變成純函數,畢竟我們終究需要 Actions 來跟世界互動。
但我們的目標,是盡可能地用純函數來打造我們應用程式的核心邏輯,並盡量提高程式碼中純函數的比例。
